Question

In the square pyramid below, the sides of the

square base measure 4 cm and the slant
height measures 8 cm. If the slant height is
tripled and the base lengths remain the same,
by how much, in square inches, will the
surface area increase?​

Answer 1

`\bigtriangleup= 19.84\ in^2`

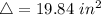
Explanation:

We calculate the initial area before the dimension modifications.

-The surface area(given the slant height) is calculated as:

`A=Base \ Area +Triangle:s \ Area\\\\=s^2+4(0.5sh)\\\\s=base \ side, h=\ slant \ height\\\\\therefore A=4^2+4(0.5* 8* 4)\\\\=80\ cm^2`

-If the slant height is tripled, the new height will be 3*8=24, and the base lengths remain unchanged:

`A_n=Base \ Area +Triangle:s \ Area\\\\=s^2+4(0.5sh)\\\\s=base \ side, h=\ slant \ height\\\\\therefore A_n=4^2+4(0.5* 24* 4)\\\\=208\ cm^2`

-The change in area is calculated as (1 sq cm=0.155 sq in):

`\bigtriangleup=A_n-A\\\\=128\ cm^2\\\\=>1 \ cm^2=0.155\ in^2\\\\\therefore 128\ cm^2=0.155\ in^2* 128\\\\=19.84\ in^2`