Answer:
There is a difference between the two means.
Explanation:
The hypothesis can be defined as:
H₀: The mean exam scores of my SAT 215 students with colorful calculators are same as the mean scores of my STA 215 students with plain black calculators, i.e. μ₁ - μ₂ = 0.
Hₐ: The mean exam scores of my SAT 215 students with colorful calculators are different than the mean scores of my STA 215 students with plain black calculators, i.e. μ₁ - μ₂ ≠ 0.
Assume that the significance level of the test is, α = 0.05. Also assuming that the population variances are equal.
The decision rule:
A 95% confidence interval for mean difference can be used to determine the result of the hypothesis test. If the 95% confidence interval contains the null hypothesis value, i.e. 0 then the null hypothesis will not be rejected.
The 95% confidence interval for mean difference is:
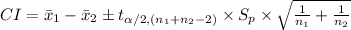
Compute the pooled standard deviation as follows:
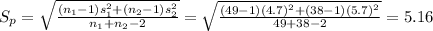
The critical value of t is:
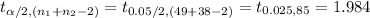
*Use a t-table.
Compute the 95% confidence interval for mean difference as follows:
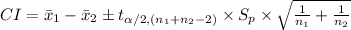
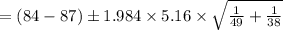
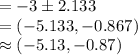
The 95% confidence interval for mean difference is (-5.13, -0.87).
The confidence interval does not contains the value 0. This implies that the null hypothesis will be rejected at 5% level of significance.
Hence, concluding that the mean exam scores of my STA 215 students with colorful calculators are different than the mean scores of my STA 215 students with plain black calculators.