Question

asked Feb 27, 2021 96.3k views

1 Answer

Mattmilten · Answer 1 · 2021-03-05T15:51:34+0000

Answer:

(a)

(i) The probability that a bulb fails within the first 500 hours is 0.3935.

(ii) The probability that a bulb burns for more than 700 hours is 0.4966.

(b) The median lifetime of the lightbulbs is 693.15 hours.

Explanation:

Let X = lifetime of a type of lightbulb.

The random variable X is Exponentially distributed with mean lifetime of, μ = 1000 hours.

The probability density function of X is:

$f_(X)(x)=\left \{ {{\lambda e^(-\lambda x);\ x\geq 0,\ \lambda>0} \atop {0;\ otherwise}} \right.$

The value of λ is:

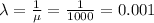
$\lambda=(1)/(\mu)=(1)/(1000)=0.001$

(i)

Compute the probability that a bulb fails within the first 500 hours as follows:

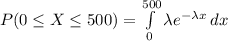
$P(0\leq X\leq 500)=\int\limits^(500)_(0){\lambda e^(-\lambda x)}\, dx\\$

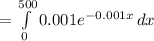
$=\int\limits^(500)_(0){0.001 e^(-0.001 x)}\, dx\\$

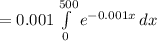
$=0.001\int\limits^(500)_(0){e^(-0.001 x)}\, dx\\$

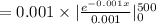
=0.001* |(e^(-0.001x))/(0.001)|^(500)_(0)

$=1-(e^(-0.001* 500)\\=1-0.6065\\=0.3935$

Thus, the probability that a bulb fails within the first 500 hours is 0.3935.

(ii)

Compute the probability that a bulb burns for more than 700 hours as follows:

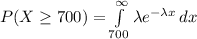
$P(X\geq 700)=\int\limits^(\infty)_(700){\lambda e^(-\lambda x)}\, dx\\$

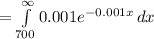
$=\int\limits^(\infty)_(700){0.001 e^(-0.001 x)}\, dx\\$

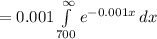
$=0.001\int\limits^(\infty)_(700){e^(-0.001 x)}\, dx\\$

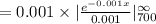
$=0.001* |(e^(-0.001x))/(0.001)|^(\infty)_(700)$

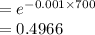
$=e^(-0.001* 700)\\=0.4966$

Thus, the probability that a bulb burns for more than 700 hours is 0.4966.

(b)

The median of an exponentially distributed random variable is:

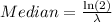
$Median=(\ln(2))/(\lambda)$

Compute the median lifetime of the lightbulbs as follows:

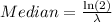
$Median=(\ln(2))/(\lambda)$

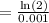
$=(\ln(2))/(0.001)$

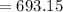
=693.15

Thus, the median lifetime of the lightbulbs is 693.15 hours.

Please log in or register to add a comment.