Question

Recall that a cube has eight corners and six square A point charge Q, placed at the center of a cube, produces an electric field strength of E — 130V/m, at each of the eight corners of the cube. What is the strength of the electric field at the centers of the six square faces of the cube?

Answer 1

First we need to determine the distance from the center of the box to each of the corners. Geometrically this distance can be defined as

`d_1= \sqrt{ ((a)/(2))^2+((a)/(2))^2+((a)/(2))^2}`

`d_1 = (√(3))/(2)a`

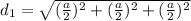
Distance between center of cube and center of face is,

`d_2 = (a)/(2)`

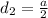
Then the Electric field will be given for each point as,

`E_1 = (kQ)/(d_1^2)`

`E_2 = (kQ)/(d_2^2)`

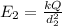
The relation between the two electric field then will be

`(E_1)/(E_2) = (d_2^2)/(d_1^2)`

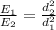
The first electric field in function of the second electric field is

`E_2 = (d_1^2E_1)/(d_2^2)`

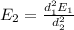
Replacing,

`E_2 = (3)/(4)*4 E_1`

`E_2 = 3E_1`

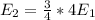
Replacing with the value given,

`E_2 = 3*(130V/m)`

`E_2 = 390V/m`

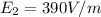
Therefore the strength of the electric field at the centers of the six square faces of the cube is 390V/m