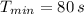Answer:
a)
Step-by-step explanation:
a) Let consider that disk accelerates and decelerates at constant rate. The expression for angular acceleration and deceleration are, respectively:
Acceleration
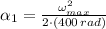
Deceleration
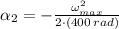
Since angular acceleration and deceleration have same magnitude but opposite sign. Let is find the maximum allowed angular speed from maximum allowed centripetal acceleration:
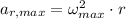
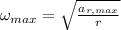

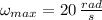
Maximum magnitude of acceleration/deceleration is:
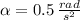
The least time require for rotation is: