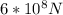Question

Radiation from the Sun reaching Earth (just outside the atmosphere) has an intensity of 1.4 kW/m2. (a) Assuming that Earth (and its atmosphere) behaves like a flat disk perpendicular to the Sun's rays and that all the incident energy is absorbed, calculate the force on Earth due to radiation pressure.

Answer 1

To solve the problem we will require the concept of Force as a definition of pressure and Area, and the concept of light pressure itself determined by the relationship between intensity and the speed at which light travels. We will match the terms and find the desired force value,

`F = PA`

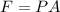
Here,

P = Pressure

A = Area

Pressure due to the light of the sun will be

`P= (I)/(c)`

Here,

I = Intensity

c = Speed velocity

Equation both therms we have that

`F = (IA)/(c)`

We have a circular area then

`F = (I(\pi r^2))/(c)`

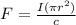
Replacing with our values (Adding the radius of the Earth)

`F = ((1.4*10^3W/m^2)(\pi (6.32*10^6m)^2))/(3.0*10^8m/s)`

`F = 6.0*10^8N`

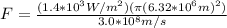
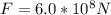
Therefore the Force on Earth due to radiation pressure is
`6*10^8N`