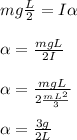Answer:
The Tension
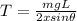
The horizontal component
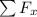 =
=
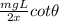
The vertical component
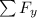 =
=
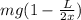
The angular acceleration ∝ =
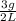
Step-by-step explanation:
The illustration of what the question depicts is shown in the diagram below;
SO; Equilibrium
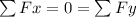
although the net torque is zero about any point ;
Now;
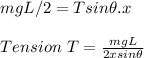
The horizontal component is :
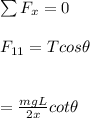
The vertical component is :
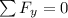
F⊥ = mg - T sin θ
=
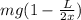
b) Torque about point 0 =