Question

1. Find a formula for the general term of the sequence, assuming the pattern continues and that the first term corresponds to , 2. Determine whether the sequence converges or diverges. If it converges, find its limit. 3. Determine whether each series is convergent or divergent. If it is convergent, find its sum.

Answer 1

1. an = (-1)^(n-1)·(n+2)!/3^n

2. the sequence diverges

Explanation:

Perhaps you're concerned with the sequence ...

{2, -24/9, 120/27, -720/81, ...}

1. This is neither arithmetic nor geometric. Ratios of terms are -4/3, -5/3, -6/3.

The alternating signs mean one factor of the general term is (-1)^(n-1). The divisors of 3 in the term ratios indicate 3^-n is another factor. The increasing multipliers suggest that a factorial is involved.

If we rewrite the sequence factoring out (-1)^(n-1)/3^n, we have ...

{6, 24, 120, 720, ...}

corresponding to 3!, 4!, 5!, 6!. This lets us conclude the remaining factor is (n+1)!.

The general term is ...

`\boxed{a_n=((-1)^(n-1)(n+2)!)/(3^n)}`

__

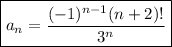
2. The magnitude of the factorial quickly outstrips the magnitude of the exponential denominator, so the terms keep getting larger and larger.

The sequence diverges.

__

3. No series are provided.