Answer:
A production level that will minimize the average cost of making x items is x=5.
Explanation:
Given that

is the cost of manufacturing x items
To find a production level that will minimize the average cost of making x items:
The average cost per item is
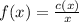
Now we get
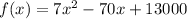
f(x) is continuously differentiable for all x
Here x≥0 since it represents the number of items.,
Put x=0 in

For x=0 the average cost becomes 13000
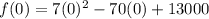
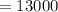
∴ f(0)=13000
To find Local extrema :
Differentiating f(x) with respect to x
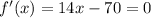
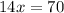
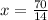
∴ x=5 gives the minimum average cost .
At x=5 the average cost is
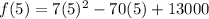
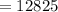
∴ f(5)=12825 which is smaller than for x=0 is 13000
∴ f(x) is decreasing between 0 and 5 and it is increasing after 5.