Question

A 300 gg ball on a 70-cmcm-long string is swung in a vertical circle about a point 200 cmcm above the floor. The string suddenly breaks when it is parallel to the ground and the ball is moving upward. The ball reaches a height 600 cmcm above the floor. Part APart complete What was the tension in the string an instant before it broke? Express your answer to two significant figures and include the appropriate units. TT = 34 NN

Answer 1

the tension in the string an instant before it broke = 34 N

Step-by-step explanation:

Given that :

mass of the ball m = 300 g = 0.300 kg

length of the string r = 70 cm = 0.7 m

At highest point, law of conservation of energy can be expressed as :

`(1)/(2) mv^2 = mgh\\\\v = √(2gh)\\\\v = √(2*(9.8 \ m/s^2)*(6.00 \ m - 2.00 \ m))\\\\`

`v = 8.854 \ m/s`

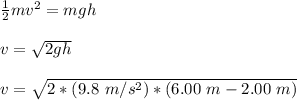
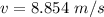
The tension in the string is:

`T = (mv^2)/(r)\\\\T = ((0.300 \ kg)*(8.854 \ m/s^2))/(0.70 \ m)\\\\T = 33.59 N\\\\T = 34 \ N`

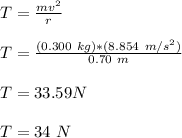
Thus, the tension in the string an instant before it broke = 34 N