Question

n order to set rates, an insurance company is trying to estimate the number of sick days that full time workers at an auto repair shop take per year. Assume σ = 6.8 days. How large a sample must be selected if the company wants to be 98% confident that the true mean differs from the sample mean by no more than 2 days?

Answer 1

The large sample must be selected if the company wants to be 98% confident that the true mean differs from the sample mean by no more than 2 days

n = 62.5427≅63

Explanation:

Step1:-

Given maximum of error = M.E = 2 days

Given population standard deviation σ = 6.8 days

98% confident level Z₀.₀₂ = 2.326

Step2:-

we know that the maximum of error

`M.E = (Z_(\alpha ) S.D )/(√(n) )`

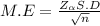
cross multiplication , we get

`√(n) = (Z_(\alpha ) S.D )/(M.E )`

squaring on both sides, we get

`n = ((Z_(\alpha ) S.D )/(M.E ))^2`

`n = ((2.326 X 6.8)/(2) )^(2)`

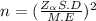
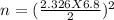
on calculation , we get

n = 62.5427

Conclusion:-

The large sample must be selected if the company wants to be 98% confident that the true mean differs from the sample mean by no more than 2 days

n = 62.5427≅63