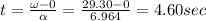Answer:
Time taken by disk to stop spinning will be 4.60 sec
Step-by-step explanation:
It is given mass m = 7.50 kg
Diameter of the disk d = 88 cm = 0.88 m
So radius of the disk
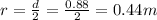
Angular speed of the disk
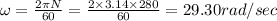
Force is given F = 35 N
Coefficient of friction
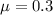
Friction force will be equal to
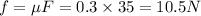
So torque will be equal to
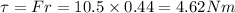
Torque is also equal to
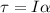
Moment of inertia of the disk

So

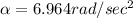
So time taken will be equal to