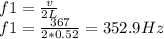Question

A pipe that is open at both ends has a fundamental frequency of 320 Hz when the speed of sound in air is 331 m/s.

Answer 1

Question

What is the length of the pipe?

Answer:

(a) 0.52m

(b) f2=640 Hz and f3=960 Hz

(c) 352.9 Hz

Step-by-step explanation:

For an open pipe, the velocity is given by

`v=\frac {2Lf}{n}`

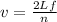
Making L the subject then

`L=\frac {nV}{2f}`

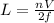
Where f is the frequency, L is the length, n is harmonic number, v is velocity

Substituting 1 for n, 320 Hz for f and 331 m/s for v then

`L=\frac {1*331}{2*320}=0.5171875\approx 0.52m`

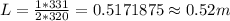
(b)

The next two harmonics is given by

f2=2fi

f3=3fi

f2=3*320=640 Hz

f3=3*320=960 Hz

Alternatively,
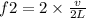`f2=2* \frac {v}{2L}` and
`f3=3* \frac {v}{2L}`

`f2=2* \frac {331}{2*0.52}=636.5 Hz\\f3=3* \frac {331}{2*0.52}=954.8 Hz`

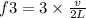
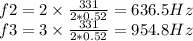
(c)

When v=367 m/s then

`f1= \frac {v}{2L}\\f1= \frac {367}{2*0.52}=352.9 Hz`