Answer:
The cartesian form of the polar equation is:
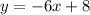
Explanation:
Start by multiplying both sides of the equal sign by the denominator on the right, so we get rid of all denominators:

Now recall the relationships for the "x" and "y" cartesian variables:
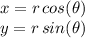
So we use this identities to replace the polar coordinates in our equation, obtaining:

Which renders a line with slope -6 and y-intercept +8