Recall that
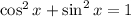 and
and
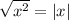 for all
for all
 . So
. So
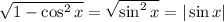

For
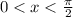 , we expect both
, we expect both
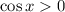 and
and
 (i.e. the sine and cosine of any angle that lies in the first quadrant must be positive). By definition of absolute value,
(i.e. the sine and cosine of any angle that lies in the first quadrant must be positive). By definition of absolute value,
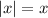 if
if
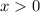 .
.
So we have
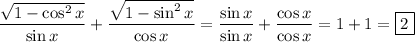
making H the answer.
C is always true, because the inequality reduces to x > y.