Question

Markus sent a chain letter to his friends, asking them to forward the letter to more friends. The relationship between the elapsed time, t tt, in days, since Markus sent the email, and the total number of people who receive the email, P ( t ) P(t)P, left parenthesis, t, right parenthesis, is modeled by the following function:

Answer 1

43% and added to

Explanation:

Answer 2

68% increase every day

Explanation:

Missing question: complete the following sentence:

Every day, there is a ....% addition to/removal from the number of people who receive the mail

The function that models the relationship between the elapsed time t (in days) and the number of people who receive the mail P(t) is:

`P(t)=(1.09)^(6t+25.5)`

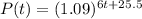
where

t is the elapsed time, in days

P(t) is the number of people who receive the mail

Here we want to find the rate of change of the function.

The rate of change of P(t) per every hour can be calculated by evaluating the ratio between P(t+1) and P(t):

`r=(P(t+1))/(P(t))`

Substituting,

`r=((1.09)^(6(t+1)+25.5))/((1.09)^(6t+25.5))=\\=((1.09)^(6t+6+25.5))/((1.09)^(6t+25.5))=\\=((1.09)^(6t+25.5)\cdot (1.09)^6)/((1.09)^(6t+25.5))=(1.09)^6=1.68`

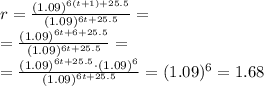
So, every day there is a 68% increase.