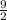Answer:
The function is f(x) =
 x +
x +
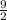
Explanation:
The point-slope form of a linear function is
 , where
, where
- m is the slope of the graph (rate of change)
- (
 ,
,
 ) is a point on the line (the line passes through it)
) is a point on the line (the line passes through it)
∵ The function has a rate of change

- The rate of change is the slope of the graph
∴ m =

∵ The graph is passes through point (4 , 10.5)
∴
 = 4 and
= 4 and
 = 10.5
= 10.5
Substitute m and the coordinates of the point in the form of the equation
∵

∴ y - 10.5 =
 (x - 4)
(x - 4)
Simplify the right hand side
∴ y - 10.5 =
 (x) -
(x) -
 (4)
(4)
∴ y - 10.5 =
 x - 6
x - 6
Add 10.5 to both sides
∴ y =
 x + 4.5
x + 4.5
∵ 4.5 =
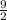
∴ y =
 x +
x +
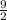
∵ y = f(x)
∴ f(x) =
 x +
x +
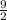
The function is f(x) =
 x +
x +