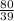Question

In ΔKLM, the measure of ∠M=90°, LK = 89, ML = 80, and KM = 39. What ratio represents the tangent of ∠K?

Answer 1

80/39

Explanation:

TanK = opposite/adjacent

TanK = LM/KM

= 80/39

Answer 2

Given:

It is given that KLM is a right triangle.

The measure of ∠M is 90°

The length of LK is 89, ML is 80 and KM is 39.

We need to determine the ratio that represents the tangent of ∠K.

Measure of tan ∠K:

The measure of tan ∠K can be determined using the trigonometric ratio.

Thus, we have;

`tan \ \theta=(opp)/(adj)`

From the figure attached below, the side opposite to ∠K is ML and the side adjacent to ∠K is KM

Hence, substituting the values, we get;

`tan \ k=(ML)/(KM)`

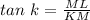
where ML = 80 and KM = 39.

Substituting, we get;

`tan \ k=(80)/(39)`

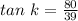
Thus, the ratio that represents the tangent of ∠K is
`(80)/(39)`