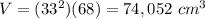Question

The Post Office used to have a strange way of limiting the size of packages. The maximum allowed was a 2 meters combined length and girth. Given this restriction, what is the greatest volume of a package that is shaped like a rectangular prism with whole centimeter dimensions? (Remember that 100 cm = 1 m)

Answer 1

`V=74,052\ cm^3`

Explanation:

we know that

The maximum volume for a rectangular prism is when the base is a square

The girth is the distance around the package perpendicular to the length

see the attached figure to better understand the problem

Let

x ----> the length of the square base of the prism

h ---> the height of the prim

we have that

`4x+h=2`

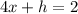
`h=2-4x` -----> equation A

The volume of a rectangular prism is given by

`V=Bh`

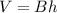
where

B is the area of the base

h is the height of the prism

we have

`B=x^2`

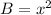
so

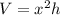`V=x^2h` ----> equation B

substitute equation A in equation B

`V=x^2(2-4x)`

`V=-4x^3+2x^2`

Find the first derivative of the function

`(dV)/(dx)=-12x^2+4x`

equate to zero

`-12x^2+4x=0\\-12x(x-(1)/(3))=0`

`x=0.33\ m` ---->
`x=33\ cm`

`h=200-4(33)=68\ cm`

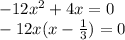
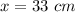
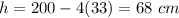
therefore

The greatest volume is equal to

`V=(33^2)(68)=74,052\ cm^3`