Answer:
19.1 ft
Explanation:
-This a Pythagorean theorem problem given by the function:
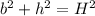
Where
H is the Hypotenuse length
h is the perpendicular height
b is the base length.
#Given that H=20 ft and base length,b =6 ft, the perpendicular height is calculated as:
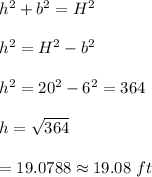
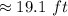
Hence, the ladder reaches the wall at a height of 19.1 ft