Question

Please help me I’m so confused

Answer 1

Given:

The given expression is
`\sum_(1)^(10) 4\left((1)/(4)\right)^(n-1)`

We need to evaluate the given expression.

Solution:

The given expression is in the form of general form of geometric sequence
`a_n=ar^(n-1)`

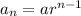
The common ratio is
`r=(1)/(4)` and the first term is a = 4.

The formula to find the sum of the series is given by

`S_n=a((1-r^(n))/(1-r))`

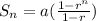
Substituting n= 10, a = 4 and
`r=(1)/(4)` , we get;

`S_(10)=4 \cdot (1-\left((1)/(4)\right)^(10))/(1-(1)/(4))`

`S_(10)=4 \cdot (1-(1)/(1048576))/(1-(1)/(4))`

`S_(10)=4 ( ((1048575)/(1048576))/((3)/(4)))`

`S_(10)=4 ( (1048575)/(1048576) * {(4)/(3))`

`S_(10)= (16777200)/(3145728)`

`S_(10)=5.33`

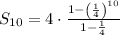
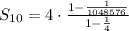
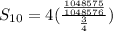
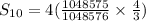
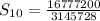
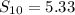
Thus, the sum of the 10 terms is 5.33