Question

Find the measure of each angle.

Answer 1

Given:

Given that the isosceles trapezoid JKLM.

The measure of ∠K is 118°

We need to determine the measure of each angle.

Measure of ∠L:

By the property of isosceles trapezoid, we have;

`\angle K+\angle L=180^(\circ)`

`118^(\circ)+\angle L=180^(\circ)`

`\angle L=62^(\circ)`

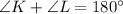
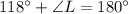
Thus, the measure of ∠L is 62°

Measure of ∠M:

By the property of isosceles trapezoid, we have;

`\angle L \cong \angle M`

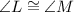
Substituting the value, we get;

`62^(\circ)=\angle M`

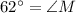
Thus, the measure of ∠M is 62°

Measure of ∠J:

By the property of isosceles trapezoid, we have;

`\angle J \cong \angle K`

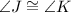
Substituting the value, we get;

`\angle J =118^(\circ)`

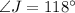
Thus, the measure of ∠J is 118°

Hence, the measures of each angles of the isosceles trapezoid are ∠K = 118°, ∠L = 62°, ∠M = 62° and ∠J = 118°