Question

You deposit ​$1000 in an account that pays 7​% interest compounded semiannually. After 4 ​years, the interest rate is increased to 7.36​% compounded quarterly. What will be the value of the account after a total of 8 ​years?

Answer 1

`\$1762.86`

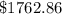
Explanation:

GIVEN: You deposit ​
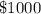`\$1000` in an account that pays
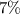`7\%` interest compounded semiannually. After
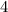`4` ​years, the interest rate is increased to
`7.36%` compounded quarterly.

TO FIND: What will be the value of the account after a total of
`8` ​years.

SOLUTION:

Total initial amount deposited in account
`=\$1000`

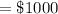
rate of interest for first
`4\text{ years}`
`=7\%`

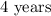
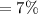
As interest compounds semiannually, it compounds twice a year

Amount generated by compound interest
`=P(1+(r)/(n))^n^t`

Here initial Principal amount
`P=\$1000`

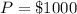
Here total duration
`nt=4\text{ years}`

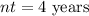
total number of times compounding done
`n=2`

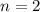
putting values

`=1000(1+(7)/(100*2))^4`

`=\$1316.81`

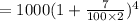
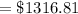
after
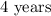`4\text{ years}` the rate is changed and the amount generated after first
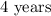`4\text{ years}` will be the new principal amount

new Principal amount
`P=\$1316.81`

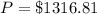
total duration
`nt=4\text{ years}`

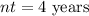
compounding done in a year
`n=4`

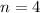
new rate of interest
`r=\$7.36\%`

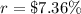
putting values in above mentioned formula

`=1316.81(1+(7.36)/(100*4))^4`

`=\$1762.86`

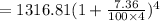
Hence after
`8` years there will be
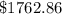`\$1762.86` in account.