Question

ACT mathematics score for a particular year are normally distributed with a mean of 28 and a standard deviation of 2.4 points

A. What is the probability a randomly selected score is greater than 30.4?

B. what is the probability a randomly selected score is less than 32.8?

C. What is the probability a randomly selected score is Between 25.6 and 32.8?

Answer 1

a. 0.1587

b. 0.8849

c. 0.1814

Explanation:

a. Given that
`\mu=28, \ \ \sigma=2.4`

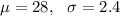
-The probability a randomly selected score is greater than 30.4 is calculated as:

`P(X>30.4)=1-P(X<30.4)\\\\z=(\bar X-\mu)/(\sigma)\\\\=(30.4-28)/(2.4)=1\\\\\therefore P(X>30.4)=1-P(z<1)\\\\=1-0.84134\\\\=0.1587`

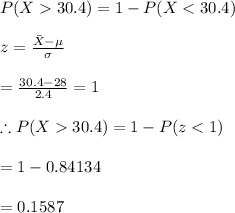
Hence, the probability of a score greater than 30.4 is 0.1587

b. Given that
`\mu=28, \ \ \ \sigma=2.4`

The probability a randomly selected score is less than 32.8 is calculated as:

`P(X<32.8)=P(z<(\bar X-\mu)/(\sigma))\\\\z=(\bar X-\mu)/(\sigma)\\\\=(32.8-28)/(2.4)=1.2\\\\P(X<32.8)=P(z<1.2)\\\\=0.88493`

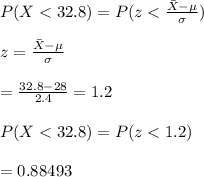
Hence, the probability that a randomly selected score is less than 32.8 is 0.8849

c. The probability that a score is between 25.6 and 32.8 is calculated as follows:

`P(25.6<X<32.8)=P((\bar X-\mu)/(\sigma)<z<(\bar X-\mu)/(\sigma))\\\\=P((25.6-28)/(2.4)<z<(32.8-28)/(2.4))\\\\=P(-1<z<2.0)\\\\=0.15866+(1-0.97725)\\\\=0.1814`

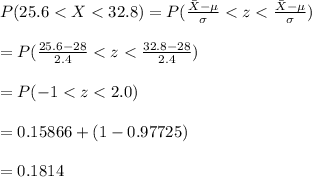
Hence, the probability is 0.1814