Given:
The diagonals of the parallelogram bisect each other.
Thus, the lengths of the diagonals of the parallelogram are (k + 4), 11, m and 8.
We need to determine the value of the variables k and m.
Value of k:
Since, we know that, the diagonals bisect each other which means that the diagonals cut each other into two equal halves.
Thus, we have;
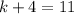

Thus, the value of k is 7.
Value of m:
Applying the same property that diagonals bisect each other. We have;
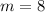
Thus, the value of m is 8.
Hence, the value of the variables k and m are 7 and 8 respectively.