Question

You have one type of nut that sells for $2.80/lb and another type of nut that sells for $5.30/lb. You would like to have 12.5 lbs of a nut mixture that sells for $3.80/lb. How much of each nut will you need to obtain the desired mixture?

Answer 1

`7.5\text{ lbs and }5\text{ lbs}`

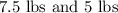
Explanation:

GIVEN: You have one type of nut that sells for
`\$2.80\text{/lb}` and another type of nut that sells for
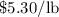`\$5.30\text{/lb}`. You would like to have
`12.5\text{ lbs}` of a nut mixture that sells for
`\$3.80\text{/lb}`

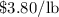
TO FIND: How much of each nut will you need to obtain the desired mixture.

SOLUTION:

Rate of first type of nut
`=\$2.80\text{/lb}`

Rate of second type of nuts
`=\$5.30\text{/lb}`

Total amount of nut mixture
`=12.5\text{ lbs}`

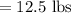
let the total quantity of first type of nut be
`=x\text{ lbs}`

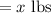
quantity of second type of nuts
`=12.5-x \text{ lbs}`

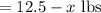
Now,

rate of new nut mixture
`=\$3.80\text{/lb}`

rate of new mixture
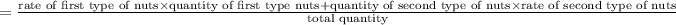`=\frac{\text{rate of first type of nuts}*\text{quantity of first type nuts}+\text{quantity of second type of nuts}*\text{rate of second type of nuts}}{\text{total quantity}}`putting values

`(2.80* x+5.3*(12.5-x))/(12.5)=3.8`

`2.8x+5.3*12.5-5.3x=12.5*3.8`

`2.5x=18.75`

`x=7.5\text{ lbs}`

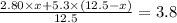
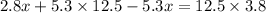
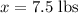
quantity of first type of nuts
`=7.5\text{ lbs}`

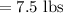
quantity of second type of nuts
`=12.5-7.5=5\text{ lbs}`

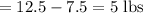
Hence
`7.5\text{ lbs}` of first type of nuts and
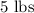`5\text{ lbs}` of second type of nuts are required to obtain the desired mixture.