Question

Lee las situaciones y realiza lo siguiente con cada una:

Escribe las magnitudes intervienen
Escribe cuál magnitud es la variable independiente y cuál la variable dependiente
Representa la función que describe la situación

SITUACIONES:

Una máquina imprime 840 páginas cada 30 minutos.
Un ascensor tarda 6 segundos para subir dos pisos.
Una empresa alquila un auto a S/ 480 por 12 días.
10 kilogramos de papaya cuesta S/ 35.

Answer 1

Part 1) see the explanation

Part 2) see the explanation

Part 3) see the explanation

Part 4) see the explanation

Explanation:

The question in English is

Read the situations and do the following with each one:

Write down the magnitudes involved

Write which magnitude is the independent variable and which is the dependent variable

It represents the function that describes the situation

SITUATIONS:

1) A machine prints 840 pages every 30 minutes.

2) An elevator takes 6 seconds to go up two floors.

3) A company rents a car at S/ 480 for 12 days.

4) 10 kilograms of papaya cost S/ 35

Part 1) we have

A machine prints 840 pages every 30 minutes

Let

x ----> the time in minutes (represent the variable independent or input value)

y ---> the number of pages that the machine print (represent the dependent variable or output value)

Remember that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
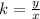`k=(y)/(x)` or
`y=kx`

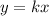
In this problem

we have a a proportional variation

so

The value of the constant of proportionality is equal to

`k=(y)/(x)`

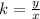
we have

`y=840\ pages\\x=30\ minutes`

substitute

`k=(840)/(30)=28\ pages/minute`

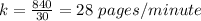
The linear equation is

`y=28x`

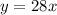
Part 2) we have

An elevator takes 6 seconds to go up two floors.

Let

x ----> the time in seconds (represent the variable independent or input value)

y ---> the number of floors (represent the dependent variable or output value)

Remember that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
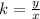`k=(y)/(x)` or
`y=kx`

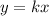
In this problem

we have a a proportional variation

so

The value of the constant of proportionality is equal to

`k=(y)/(x)`

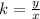
we have

`y=2\ floors\\x=6\ seconds`

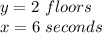
substitute

`k=(2)/(6)=(1)/(3)\ floors/second`

The linear equation is

`y=(1)/(3)x`

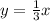
Part 3) we have

A company rents a car at S/ 480 for 12 days.

Let

x ----> the number of days (represent the variable independent or input value)

y ---> the cost of rent a car (represent the dependent variable or output value)

Remember that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
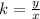`k=(y)/(x)` or
`y=kx`

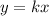
In this problem

we have a a proportional variation

so

The value of the constant of proportionality is equal to

`k=(y)/(x)`

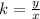
we have

`y=\$480\\x=12\ days`

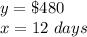
substitute

`k=(480)/(12)=\$40\ per\ day`

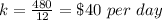
The linear equation is

`y=40x`

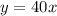
Part 4) we have

10 kilograms of papaya cost S/ 35

Let

x ----> the kilograms of papaya (represent the variable independent or input value)

y ---> the cost (represent the dependent variable or output value)

Remember that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
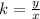`k=(y)/(x)` or
`y=kx`

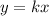
In this problem

we have a a proportional variation

so

The value of the constant of proportionality is equal to

`k=(y)/(x)`

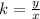
we have

`y=\$35\\x=10\ kg`

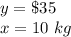
substitute

`k=(35)/(10)=\$3.5\ per\ kg`

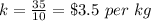
The linear equation is

`y=3.5x`