Question

The area of a circular base of the larger cylinder is 81 pie

The area of a circular base of the smaller cylinder is 9 pie
Make a conjecture about the similar solids. How is the
scale factor and the ratio of the surface areas related?
Check all that apply.
The dimensions of the larger cylinder are 3 times
the dimensions of the smaller cylinder.
The surface area of the larger cylinder is 32. or 9.
times the surface area of the smaller cylinder
If proportional dimensional changes are made to a
solid figure, then the surface area will change by
the square of the scale factor of similar solids.

Answer 1

On edg it doesnt matter just select nothing and it will say ur right. But only if its asking for a conjecture. So no matter what you select it will be right

<3

Explanation:

Answer 2

The dimensions of the larger cylinder are 3 times the dimensions of the smaller cylinder

The surface area of the larger cylinder is 3^2. or 9 times the surface area of the smaller cylinder

If proportional dimensional changes are made to a solid figure, then the surface area will change by the square of the scale factor of similar solids

Explanation:

we know that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Let

z ----> the scale factor

x ----> the area of the base of larger cylinder

y ---> the area of the base of smaller cylinder

so

`z^(2) =(x)/(y)`

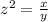
we have

`x=81\pi\ units^2`

`y=9\pi\ units^2`

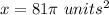
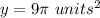
substitute

`z^(2) =(81\pi)/(9\pi)`

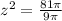
solve for z

`z^2=9\\z=3`

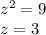
Verify each statement

1) The dimensions of the larger cylinder are 3 times the dimensions of the smaller cylinder

The statement is true

Because the scale factor is equal to 3 ( see the explanation)

2) The surface area of the larger cylinder is 3^2. or 9 times the surface area of the smaller cylinder

The statement is true

Because, the surface area of the larger cylinder is equal to the surface area of the smaller cylinder multiplied by the scale factor squared

3) If proportional dimensional changes are made to a solid figure, then the surface area will change by the square of the scale factor of similar solids

The statement is true

because

If two figures are similar, then the ratio of its areas is equal to the scale factor squared