Question

What is the measure of? angle PQR
[Not drawn to scale)
-51
-55
-74
-78

Answer 1

Explanation:

Answer 2

Given:

The exterior angle P is 74°

The measure of ∠PRQ is 51°

We need to determine the measure of ∠PQR

Measure of ∠QPR:

From the figure, it is obvious that P is the intersection of the two lines.

The angle 74° and ∠QPR are vertically opposite angles.

Since, vertically opposite angles are always equal, then the measure of ∠QPR is 74°

Thus, the measure of ∠QPR is 74°

Measure of ∠PQR:

The measure of ∠PQR can be determined using the triangle sum property.

Thus, we have;

`\angle PQR+\angle QPR+\angle PRQ=180^(\circ)`

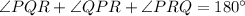
Substituting the values, we get;

`\angle PQR+74^(\circ)+51^(\circ)=180^(\circ)`

`\angle PQR+125^(\circ)=180^(\circ)`

`\angle PQR=55^(\circ)`

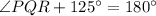
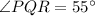
Thus, the measure of ∠PQR is 55°

Hence, Option B is the correct answer.