Question

In a random sample of 535 people 65% said they like cookies with chocolate chips 37% like cookies with peanut butter chips. 25% like cookies with both chocolate and peanut butter chips. What is the probability that a randomly selected person likes cookies with chocolate or peanut butter chips

Answer 1

The probability that a randomly selected person likes cookies with chocolate or peanut butter chips is 0.77.

Explanation:

Here, the total sample of people has total 535 people.

The percentage of people liking chocolate chip cookies = 65%

Now, 65% of 535 =
`(65)/(100) * 535 = 347.75 \approx 348`

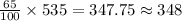
⇒ 348 people in total like chocolate chip cookies.

⇒ n(C) = 348

The percentage of people liking peanut butter chip cookies = 37%

Now, 37% of 535 =
`(37)/(100) * 535 = 197.95 \approx 198`

⇒ 198 people in total like peanut butter chip cookies.

⇒ n(B) = 198

Percentage of people liking both chocolate &peanut butter chips = 25%

Now, 25% of 535 =
`(25)/(100) * 535 =133.75 \approx 134`

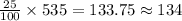
⇒ 134 people in total like both chocolate &peanut butter chips

⇒ n(C ∩ B ) = 134

Now, n( C U B) = N(C) + n(B) - n(C ∩ B )

= 348 + 198 - 134 = 412

P( person likes cookies with chocolate or peanut butter chips)

=
`\frac{\textrm{person likes cookies with chocolate or peanut butter chips}}{\textrm{Total People}} = (412)/(535) = 0.77`

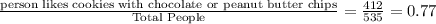
Hence, the probability that a randomly selected person likes cookies with chocolate or peanut butter chips is 0.77.