Question

An amusement park charges $17 for each adult ticket and $6 for each child ticket. One day, the park earned $3,640 in ticket sales. Let x represent the number of adult tickets sold. Let y represent the number of child tickets sold. If 400 tickets were sold on this day, which system of equations can be used to find the number of each type of ticket sold?

Answer 1

The system of equation is

x+y=400

and

17x+6y=3640

Explanation:

Given that, an amusement park charges $17 for each adult ticket and $6 for each child ticket.

Assume that, x represent the number of adult tickets sold and y represent the number of child tickets sold.

Total number of ticket sold= x+y

The park eared = $(17x+6y) in ticket sale.

According to the problem,

x+y=400 ........(1)

and

17x+6y=3640 .......(2)

Subtract equation (2) from 17 times of equation (1)

17x+17y-(17x+6y)=6,800-3640

⇒17x+17y-17x-6y=3,160

⇒11y=3160

`\Rightarrow y=(3160)/(11)`

`\Rightarrow y=287.27`

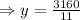
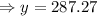
Putting the value of y in equation (1)

x+287.27=400

⇒x=112.73

The system of equation is

x+y=400

and

17x+6y=3640