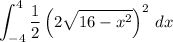The equation for the base is that of a circle, so the cross sections will have a leg of length equal to the vertical distance between its halves.
x² + y² = 16 ⇒ y = ±√(16 - x²)
⇒ length = √(16 - x²) - (-√(16 - x²)) = 2 √(16 - x²)
Cross sections with thickness ∆x have a volume of
1/2 length² ∆x = 1/2 (2 √(16 - x²))² ∆x = (32 - 2x²) ∆x
since they are isosceles triangles and so their bases and heights are equal.
Then the total volume would be (D)