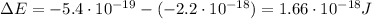a)
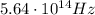
b)
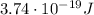
c)
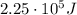
d)
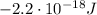
e)
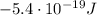
f)
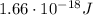
Step-by-step explanation:
a)
The frequency and the wavelength of a light wave are related by the so-called wave equation:
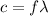
where
c is the speed of light
f is the frequency of light
 is the wavelength
is the wavelength
In this problem, we have:
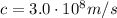 is the speed of light
is the speed of light
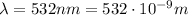 is the wavelength of the green light emitted by the laser
is the wavelength of the green light emitted by the laser
Solving for f, we find the frequency:

b)
The energy of a photon is given by the equation:
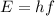
where
E is the energy
h is the Planck constant
f is the frequency of the photon
For the photon in this problem we have:
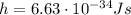 is the Planck's constant
is the Planck's constant
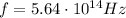 is the frequency of the photon
is the frequency of the photon
Substituting, we find the energy of the photon:
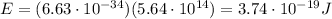
c)
1 mole of a substance is the amount of substance that contains a number of particles equal to Avogadro number:
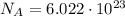
This means that 1 mole of photons will contain a number of photons equal to the Avogadro number.
Here, we know that the energy of a single photon is
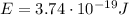
Therefore, the energy contained in one mole of photons of this light will be
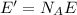
And substituting the two numbers, we get:
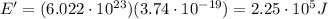
d)
According to the Bohr's model, the orbital energy of an electron in the nth-level of the atom is
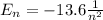 [eV]
[eV]
where
n is the level of the orbital
The energy is measured in electronvolts
In this problem, we have an electron in the ground state, so
n = 1
Therefore, its energy is
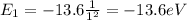
And given the conversion factor between electronvolts and Joules,
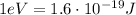
The energy in Joules is
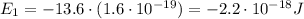
e)
As before, the orbital energy of an electron in the hydrogen atom is
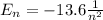 [eV]
[eV]
where:
n is the level of the orbital
The energy is measured in electronvolts
Here we have an electron in the
n = 2 state
So its energy is
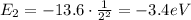
And converting into Joules,
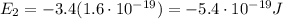
f)
The energy required for an electron to jump from a certain orbital to a higher orbital is equal to the difference in energy between the two levels, so in this case, the energy the electron needs to jump from the ground state (n=1) to the higher orbital (n=2) is:
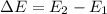
where:
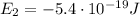 is the energy of orbital n=2
is the energy of orbital n=2
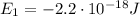 is the energy of orbital n=1
is the energy of orbital n=1
Substituting, we find: