The area of the shaded sector of the circle is 27
 units squared, if the line segments KL and ML are radii, the length of KL is 9 units and MLK is 120 degrees.
units squared, if the line segments KL and ML are radii, the length of KL is 9 units and MLK is 120 degrees.
Explanation:
The given is,
K L and M L are radii
Length of K L is 9
Angle M L K is 120 degrees
In the given question diagram is missing, so we attach the diagram.
Step:1
The shaded area of sector in the circle is
 of circle area.
of circle area.
( Three times of 120° equal to 360°)
Formula for area of circle,
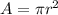 .........................................(1)
.........................................(1)
From the ratio and area of circle formula for shaded sector is,
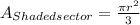 .........................(2)
.........................(2)
Where, r - radius of circle
From the given,
r = 9 units
Equation (2) becomes,


= 27

 Units squared
Units squared
Result:
The area of the shaded sector of the circle is 27
 units squared, if the line segments KL and ML are radii, the length of KL is 9 units and MLK is 120 degrees.
units squared, if the line segments KL and ML are radii, the length of KL is 9 units and MLK is 120 degrees.