Answer:
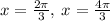
Explanation:
Alright so being presented with this equation the first thing we want to do is subtract 1 from both sides of
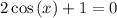 .
.
 .
.
Now we want to simplify it to
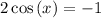 .
.
Now go ahead and divide both sides by 2.
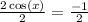
Make sure you simplify again to get
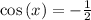 .
.
Now you need your sin/cos periodicity table. When you look at the charts. Look for the general solutions of
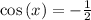 . After looking at the chart you will find
. After looking at the chart you will find
 .
.
Which we can then finalize at
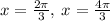 .
.
Hope this helps!