Question

Identify the values a, b, and c is the first step in using the quadratic formula to find the solution(s) to a quadratic equation. What are the values a, b, and c in the following quadratic equation? 18=-9x+7x2

Answer 1

-7, 9, 18

Explanation:

Answer 2

The values are a = 7, b = -9, c = -18.

Explanation:

The given quadratic equation is
`7x^(2) - 9x = 18`

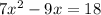
The general form of the quadratic equation is
`ax^(2) + bx + c = 0`

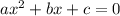
where,

• a is the coefficient of x².
• b is the coefficient of x.
• c is the constant term.

Now, you have to modify the given quadratic equation similar to the general form of quadratic equation.

So, bring the constant term 18 to the left side of the equation for equating it to zero.

⇒
`7x^(2) - 9x - 18 = 0`

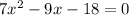
Compare the above equation with general form
`ax^(2) + bx + c = 0`

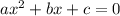
⇒ a = 7

⇒ b = -9

⇒ c = -18

Therefore, the values of a, b, and c are 7, -9 and -18.