Answer:
t=64
Explanation:
L.C.M. of 2 and 3=6

By synthetic division.
2| 1 1 0 -12
| 2 6 12
-------------------
1 3 6|0
x²+3x+6=0
disc.=b²-4ac=3²-4×1×6=9-24=-15<0
so roots are imaginary.
x=2
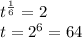
if the statement is as given by Sadievigil then he or she is correct otherwise refer to my solution.