Question

Which of the following equations are equations of circles? Choose all that apply

(x+5)2 + (y + 2)2 = -4
2x2 + y2 +15x – y + 3 = 0
x2 + y2 + 2x+10y-5=0
3x2 + 3y2 + 12x +30y - 6 = 0
x2 - y2 + 20x + 2y +9= 0

Answer 1

Explanation:

The work form of a circle is

`(x-h)^2+(y-k)^2=r^2`

The standard form of a circle is

`Ax^2+Bxy+Cy^2+Dx+Ey+F=0`

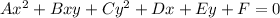
This standard form is a circle if A and C are the same number, there is a plus sign in between the x-squared and the y-squared terms, and the F value, when moved to the other side of the equals sign, is not negative. That F value represents the radius which is a measure of distance, and distances cannot be negative.

Looking at the first choice in your list, on the right side of the equals sign we have a negative 4. That means that that equation is not a circle.

Looking at the second choice in your list, we have a 2x^2 and a y^2, where A = 2 and C = 0. This is not a circle, either, since A and C have to be the same number in a circle, and they are not.

Looking at the third choice in your list, we have x^2 and y^2 with the same A and C value of 1, and if we move the F value of -5 over, we have a radius of 5, and there is a + sign in between the x^2 and the y^2 terms. Choice 3 is a circle.

Looking at the fourth choice, we have that A = 3 and C = 3, there is a + sign in between the x^2 and the y^2 terms, and if we move the -6 over to the other side, the radius is a positive number. Choice 4 is also a circle.

Looking at the last choice, there is a - sign in between the x^2 and the y^2 terms. Even though A and C are both the same number, 1, the - sign makes that possibly a hyperbola, but definitely NOT a circle.