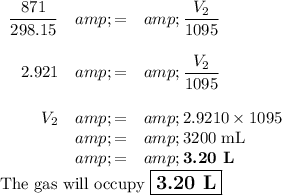Answer:
Step-by-step explanation:
The pressure and the number of moles are constant, so, to calculate the volume, we can use Charles' Law.
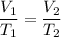
(a) Volume at -5 °C
Data:
V₁ = 871mL; T₁ = 25 °C
V₂ = ?; T₂ = -5 °C
Calculations:
(i) Convert temperatures to kelvins
T₁ = ( 25 + 273.15) K = 298.15 K
T₂ = (-5 + 273.15) K = 268.15 K
(ii) Calculate the new volume
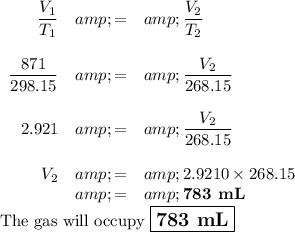
(b) Volume at 95 °F
95 °F = (95 - 32) × 5/9 = 63 × 5/9 = 35 °C
35 °C = (35 + 273.15) K = 308.15 K

(c) Volume at 1095 K