Answer:
Volume for any
 in
in
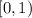 is
is
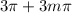 .
.
Volume for
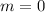 is
is
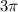 .
.
We get the same thing using the formula (volume of cylinder formula) for
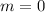 . (See below.)
. (See below.)
Step-by-step explanation:
Introduction:
 (Notice we will be filling the 3d-solid with area of a circles on the given interval.)
(Notice we will be filling the 3d-solid with area of a circles on the given interval.)
The problem is we have a hole in our 3d-solid we will need to subtract it out.
Formula:
The formula for calculating this volume will be:

The radius,
 is for bigger circle.
is for bigger circle.
The radius,
 is for smaller circle.
is for smaller circle.
What are the radi?:
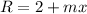
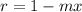
What are the radi squared?:
I will use the identity,
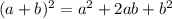 to find the square of each radius.
to find the square of each radius.
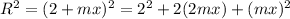
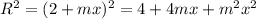
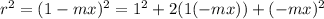
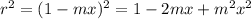
What is the positive difference of the radi squared?:
Let's find
 .
.
![R^2-r^2=[4+4mx+m^2x^2]-[1-2mx+m^2x^2]](https://img.qammunity.org/2021/formulas/mathematics/college/r06131exr5vby88vcq2ub02n2ejui92efa.png)
![R^2-r^2=[4-1]+[4mx-(-2mx)]+[m^2x^2-m^2x^2]](https://img.qammunity.org/2021/formulas/mathematics/college/yki02pj7jicpl3slbflqe0i8bfv5a06i5k.png)
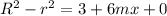
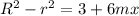
Finding the volume for any
 in
in
 :
:

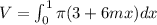
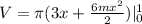
![V=\pi \{[(3(1)+(6m(1)^2)/(2)]-[3(0)+(6m(0)^2)/(2)]\}](https://img.qammunity.org/2021/formulas/mathematics/college/ndzv9xsjev78ge2dmiz1m1f74305rvawbd.png)
![V=\pi \{[3+3m]-[0+0] \}](https://img.qammunity.org/2021/formulas/mathematics/college/wwviezlitd8foe5qme6zrv3ankhlrgnzz2.png)
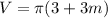
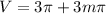
Finding the volume for
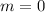 :
:
At
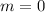 , we have
, we have
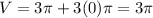 .
.
Confirmation using the volume of cylinder for
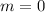 :
:
If
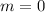 , then we have horizontal lines
, then we have horizontal lines
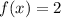 and
and
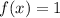 .
.
The 3d-figure that results will be a cylinder with a hole in it (that is also in the shape of a cylinder).
The larger cylinder has a radius of 2 units. So the volume of it is
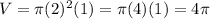 .
.
The smaller cylinder has a radius of 1 units. So the volume of it is
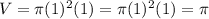 .
.
The difference of these cylinder’s volume will give us desired volume of the resulting 3d-figure which is
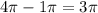 units cubed.
units cubed.
Conclusions:
Volume for any
 in
in
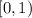 is
is
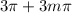 .
.
Volume for
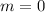 is
is
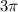 .
.
We get the same thing using the formula (volume of cylinder formula) for
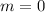 . (See above.)
. (See above.)