Answer:
Choice A: Only one equation will be sufficient for describing
 as in
as in
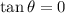 .
.
For
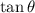 to be equal to
to be equal to
 ,
,
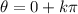 where
where
 is a whole number (including zero or negative values.)
is a whole number (including zero or negative values.)
There are two specific solutions for
 on the interval
on the interval
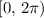 :
:
Explanation:
In a right triangle, the tangent of an angle (other than the right angle) is equal to
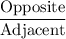 .
.
In general, if
 corresponds to the point
corresponds to the point
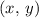 on the unit circle, then
on the unit circle, then
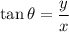 .
.
This question asks that
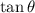 shall be zero. In other words,
shall be zero. In other words,
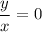 . The
. The
 -coordinate is the denominator and can't be zero. The only possibility is that the
-coordinate is the denominator and can't be zero. The only possibility is that the
 -coordinate is zero. Graphically, there are two places on a unit circle where that could happen. (Wherefore the
-coordinate is zero. Graphically, there are two places on a unit circle where that could happen. (Wherefore the
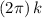 ? On a unit circle, each turn is
? On a unit circle, each turn is
 radians. The angle would appear to land at the exact same position after one or more complete turns of
radians. The angle would appear to land at the exact same position after one or more complete turns of
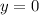 at
at
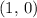 , the intersection of the unit circle and the positive
, the intersection of the unit circle and the positive
 -axis. At that point,
-axis. At that point,
 .
.
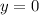 at
at
 ,the intersection of the unit circle and the negative
,the intersection of the unit circle and the negative
 -axis. At that point,
-axis. At that point,
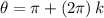 .
.
Note that these two values are separated by exactly
 radians. In other words, there is a zero every time
radians. In other words, there is a zero every time
 goes through a half circle. After
goes through a half circle. After
 , there's
, there's
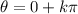 .
.
On the range
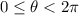 ,
,
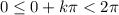 .
.
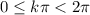 .
.
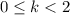 .
.
In other words,
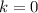 or
or
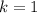 . That corresponds to
. That corresponds to
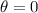 and
and
 .
.