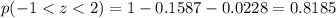Question

ACT mathematics score for a particular year are normally distributed with a mean of 28 and a standard deviation of 2.4 points

A. What is the probability a randomly selected score is greater than 30.4?

B. what is the probability a randomly selected score is less than 32.8?

C. What is the probability a randomly selected score is Between 25.6 and 32.8?

Answer 1

A) 0.1587

B) 0.9772

C) 0.8185

Explanation:

A)

In this problem, the mathematics score of the year is distributed according to a normal distribution, with parameters:

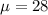`\mu=28` is the mean of the distribution

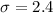`\sigma = 2.4` is the standard deviation of the distribution

We want to find the probability that a randomly selected score is greater than 30.4. First of all, we calculated the z-score associated to this value, which is given by:

`z=(30.4-\mu)/(\sigma)=(30.4-28)/(2.4)=1`

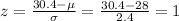
The z-score tables give the probability that the z-score is less than a certain value; since the distribution is symmetrical around 0,

`p(z>Z) = p(z<-Z)`

Here we want to find
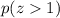`p(z>1)`, which is therefore equivalent to
`p(z<-1)`. Looking at the z-tables, we find that

`p(z<-1)=0.1587`

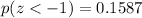
B)

Here instead we want to find the probability that a randomly selected score is less than 32.8.

First of all, we calculate again the z-score associated to this value:

`z=(32.8-\mu)/(\sigma)=(32.8-28)/(2.4)=2`

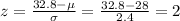
Now we notice that:

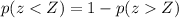`p(z<Z) = 1-p(z>Z)` (1)

Since the overall probability under the curve must be 1. We also note that (from part A)

`p(z>Z) = p(z<-Z)`

Which means that we can rewrite (1) as

`p(z<Z) = 1-p(z<-Z)`

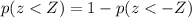
Here, we have

Z = 2

This means that

`p(z<2)=1-p(z<-2)`

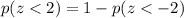
Looking at the z-tables, we find that

`p(z<-2)=0.0228`

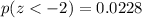
Therefore, we get

`p(z<2)=1-0.0228=0.9772`

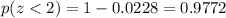
C)

Here we want to find the probablity that the score is between 25.6 and 32.8.

First of all, we calculate the z-scores associated to these two values:

`z_1=(25.6-\mu)/(\sigma)=(25.6-28)/(2.4)=-1`

`z_2=(32.8-\mu)/(\sigma)=(32.8-28)/(2.4)=2`

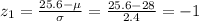
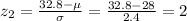
So here we basically want to find the probability that

`p(z_1 <z<z_2)`

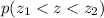
Which can be rewritten as:

`p(z_1<z<z_2)=1-p(z<z_1)-p(z>z_2)`

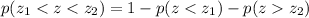
So in this case,

`p(-1<z<2)=1-p(z<-1) -p(z>2)`

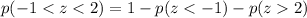
From part A and B we found that:

`p(z<-1)=0.1587`

`p(z>2)=1-p(z<2)=1-0.9772=0.0228`

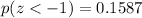
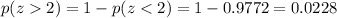
Therefore,

`p(-1<z<2)=1-0.1587-0.0228=0.8185`