Answer:
20
Explanation:
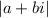 is a value that represent the distance between the points
is a value that represent the distance between the points
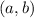 and
and
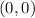 .
.
The horizontal distance is
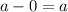 .
.
The vertical distance is
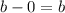 .
.
The distance between
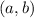 and
and
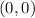 by Pythagorean Theorem is:
by Pythagorean Theorem is:
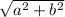 .
.
-------
Conclusion:
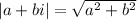 .
.
You can use that to find each of your | | terms in your problem.
However,
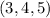 is a well remember Pythagorean Triple.
is a well remember Pythagorean Triple.
A Pythagorean Triple are three natural numbers satisfying
 .
.
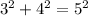 is true since
is true since
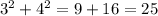 while
while
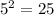 . Both sides are 25.
. Both sides are 25.
-----------------------------
If you don't like, just use the formula I mentioned once.

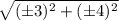
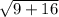
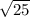

--------------------------------
The problem becomes 5+5+5+5=4(5)=20.