Question

A uniform solid sphere rolls down an incline. (a) What must be the incline angle (deg) if the linear acceleration of the center of the sphere is to have a magnitude of 0.063g? (b) If a frictionless block were to slide down the incline at that angle, would its acceleration magnitude be more than, less than, or equal to 0.063g? (a) Number Enter your answer in accordance to item (a) of the question statementEntry field with incorrect answer 27 Units Choose the answer from the menu in accordance to item (a) of the question statementEntry field with correct answer

Answer 1

the inclination of the incline angle θ = 5.06°

the acceleration magnitude is said to remains the same

Step-by-step explanation:

The acceleration of the uniform solid sphere down the incline can be illustrated as:

`a = (gsin \theta )/(1 + (k^2)/(r^2))`

where k = radius of gyration ; and for solid sphere ; k =
`((2)/(5))^2`

∴

`a = (gsin \theta )/(1 + ((2)/(5)r^2 )/(r) )`

`a = ((5)/(7))g \ sin \theta`

If the linear acceleration of the center of the sphere is to have a magnitude of 0.063 g; Then; we have:

0.063 g =
`((5)/(7))g \ sin \theta`

0.063 = 0.7143 sin θ

sin θ =
`(0.063)/(0.7143)`

sin θ = 0.0882

θ = sin⁻¹ (0.0882)

θ = 5.06°

Thus; the inclination of the incline angle θ = 5.06°

b) From the question ; the block is said to be friction-less , therefore with that, the acceleration magnitude remains the same since it contains no friction related terms.

Answer 2

(a) 12.25 °

(b) The acceleration magnitude will be more than 0.063·g or 0.212·g

Step-by-step explanation:

(a) Here we have

V = u + at

And KE = KE
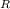`_R` + KE
`_T` = 0.5 m·v² + 0.5 Iω²

I = 2/3m·r², ω = v/r

KE = 0.5 m·v² + 2/3 m·r²·v/r

Therefore = 0.5 m·v² + 2/3 m·r·v

Therefore, v is reduced by

v = √(g·h·10/7) or v² = g·h·10/7 compared to v² = 2gh

If a = 0.063 g we have

v² = 0.063·g·h·10/7 = 0.09·g·h hence the height which is

v = 0.3√(g·h) and v = √(2·g·h)

Therefore, the angle is

sin⁻¹ (0.3/√2) = 12.25 °

v = u + at where

h = ut + 0.5at²

(b) At that angle, we have

h₁ = 0.5gt² and

h₂ = 0.212 × h₁

Therefore

a = 0.212 g, the acceleration will be more than 0.063·g.