1)
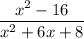
Decompose the numerator and denominator into multipliers
To simplify the numerator we use the formula of difference of squares
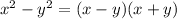

To decompose the denominator into multipliers solve the square equation
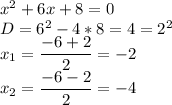
Formula for factoring a square equation
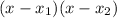
Substituting the found roots of the equation into the formula

After simplifying the numerator and denominator we get a fraction
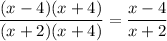 , so
, so
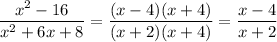
2)
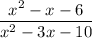
Decompose the numerator and denominator into multipliers
To decompose the numerator into multipliers solve the square equation
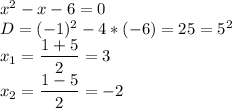
Formula for factoring a square equation
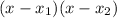
Substituting the found roots of the equation into the formula
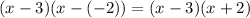
To decompose the denominator into multipliers solve the square equation

Formula for factoring a square equation
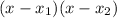
Substituting the found roots of the equation into the formula

After simplifying the numerator and denominator we get a fraction
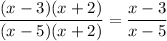 , so
, so
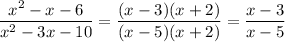
Hello from Russia:^)