Question

Find the average rate of change of f(x) = 2x^2+6

a) from 2 to 4
b) from 1 to 3
c) from -2 to 1

* THE ANSWERS ARE ON PIC but I need to know how to solve them step by step*

Answer 1

Given:

`f(x)=2 x^(2)+6`

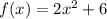
To find:

The average rate of change.

Solution:

Average rate of change formula:

`$(f(b)-f(a))/(b-a)`

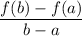
(a) Average rate of change from 2 to 4:

Substitute x = 4 and x = 2 in f(x).

`$(f(4)-f(2))/(4-2)=((2(4)^2+6)-(2(2)^2+6))/(4-2)`

`$=(38-14)/(2)`

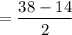
= 12

Average rate of change from 2 to 4 is 12.

(b) Average rate of change from 1 to 3:

Substitute x = 3 and x = 1 in f(x).

`$(f(3)-f(1))/(3-1)=((2(3)^2+6)-(2(1)^2+6))/(3-1)`

`$=(24-8)/(2)`

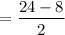
= 8

Average rate of change from 2 to 4 is 8.

(c) Average rate of change from -2 to 1:

Substitute x = 1 and x = -2 in f(x).

`$(f(1)-f(-2))/(1-(-2))=((2(1)^2+6)-(2(-2)^2+6))/(1+2)`

`$=(8-14)/(3)`

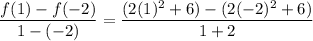
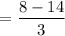
= -2

Average rate of change from 2 to 4 is -2.