Answer: A
Explanation:
Take 2 equations that make one of their letters disappear, and add them up:
2x + y + z = 1
x - y + 4z = 0
------------------------
3x + 5z = 1
Do the same with another 2 equations in which the letter, in this case y, can be removed. If you can't, take 2 of 3 equations and equal the value of the letter to make it eliminable.
x - y + 4z = 0
x + 2y - 2z = 3
Since we can't eliminate y, we have multiply as necessary to make it eliminable:
2 (x - y + 4z = 0)
= 2x - 2y + 8z = 0
add all up:
2x - 2y + 8z = 0
x + 2y - 2z = 3
-----------------------------
3x + 6z = 3
Now we've gone from a 3-variable equation to a 2-variable equation.
3x + 5z = 1
3x + 6z = 3
We can solve again by elimination; to get rid of z, for example, we cross multiply. the upper equation by 6 and the lower equation by 5. However, we have to make one of them negative in order to make them eliminable.
6 (3x + 5z = 1)
-5 (3x + 6z = 3)
----------------------------
18x + 30z = 6
-15x - 30z = -15
---------------------------
3x = - 9
Solving for x;
x =
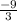
x = - 3
After finding one variable, we can use our 2-variable equations to find the next variable:
3x + 5z = 1
3 (-3) + 5z = 1
- 9 + 5z = 1
5z = 1 + 9
5z = 10
z =

z = 2
Having found these 2 variables, we can put them into one of our main 3-variable equations to find the last one:
2x + y + z = 1
2(-3) + y + 2 = 1
- 6 + y + 2 = 1
y - 4 = 1
y = 1 + 4
y = 5
And you've found all the variables in the equation; to prove if they're correct or not, you can replace them in any of the main equations and the result should be equal to each other:
x + 2y - 2z = 3
-3 + 2(5) - 2(2) = 3
- 3 + 10 - 4 = 3
10 - 7 = 3
3 = 3