Given:
The composite figure consists of a square and three semicircles.
Given that the half of the side of the square is 2 cm.
From the figure, the other half of the same side is also equal, then the side of the square is 2 + 2 = 4 cm.
We need to determine the area of the composite figure.
Area of the square:
The area of the square can be determined using the formula,
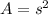
where s is the side length of the square.
Substituting s =4 ,we get;

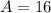
Thus, the area of the square is 16 cm²
Area of the semicircle:
The area of the semicircle can be determined using the formula,
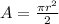
The radius of the semicircle is 2 cm.
Substituting r = 2 in the above formula, we get;
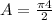
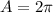
Thus, the area of the semicircle is 2π
Area of the composite figure:
The area of the composite figure can be determined by adding the area of the square and the three semicircles.
Thus, we have;
Area = Area of square + (3 × Area of semicircle)
Substituting the values, we have;

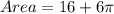
Thus, the area of the composite figure is

Hence, Option b is the correct answer.