Question

Consider two pyramids.

The first pyramid has an equilateral triangle as its base. The side length of the base is 8 units and the lateral faces each have a height of
10 units.
The second pyramid has a square as its base. The side length of the base is 6 units and the lateral faces each have a height of 12 units.
The two pyramids have equal surface area.
The surface area of the square pyramid is 180 square units.
The lateral area of the triangular pyramid is 320 square units.
The base area of the square pyramid is half the lateral area ?f the triangular pyramid.
Geog
The base area of the triangular pyramid is larger than the base area of the square pyramid.
Geor
The lateral area of the square pyramid is larger than the lateral area of the triangular pyramid.

Answer 1

• SA of square pyramid is 180 sq. units.

• Base Area of the triangular pyramid is larger that the base area of the square pyramid
• LA of SQ. pyramid is larger than the LA of the triangular pyramid are the correct statements regarding the given figures.

Explanation:

Surface Area of the given pyramids can be found using the formula as,

SA = A +
`$(1)/(2)` ps

Where SA is the surface area

A is the area of the base

p is the perimeter of the base

s is the slant height

Area of the triangle =
`$(1)/(2) * bh \\`

=
`$(1)/(2) * 8* 10`

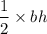
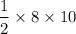
= 40 sq. units

Perimeter of the triangle = 8 + 8 + 8 = 24 units

SA of triangular pyramid = 40 + (0.5 ×24×10)

= 160 sq. units

For square pyramid,

SA of square pyramid = 36 + (0.5 × 24 × 12)

= 180 sq. units

Lateral area of triangular pyramid = perimeter × slant height / 2

= 24 × 10 × 0.5

= 120 sq. units

LA of square pyramid = 24×12×0.5 = 144 sq. units