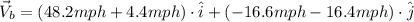Question

A hot air balloon is moving on a bearing of 134 degrees at 47 mph. Find the component form of the velocity of the balloon.

A hot air balloon is moving on a bearing of 341 degrees at 51 mph. A wind is blowing with the bearing of 285 degrees at 17 mph. Find the component form of the velocity of the balloon.

Answer 1

Question 1:

`\vec V=-32.6mph\cdot \hat i+33.8mph\cdot \hat j`

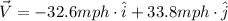
Question 2:

`\vec V_b=52.6mph\hat i-33.0mph\hat j`

Step-by-step explanation:

1. Balloon moving at 47 mph on a bearing of 134º

The x-component of a vector is the magnitude of the vector multiplied by the cosine of the angle.

The y-component of a vector is the magnitufe of the vector multiplied by the sine of the angle.

`\vec V=47mph\cdot cos(134\º)\hat i+47mph\cdot sin(134\º)\hat j`

`\vec V=-32.6mph\cdot \hat i+33.8mph\cdot \hat j`

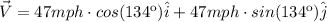
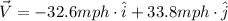
2. Balloon moving at 51mph on a bearing of 341º, with a wind blowing at 17mph on a bearing of 285º

First find, the component forms of the initial velocity of the balloon and of the wind. Then, add the two velocities.

i) Initial velocity of the balloon: Vb,i

`\vec V_(b,i)=51mph\cdot cos(341\º) \hat i+51mph\cdot sin(341\º)\hat j`

`\vec V_(b,i)=48.2mph\cdot \hat i-16.6mph\cdot \hat j`

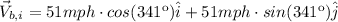
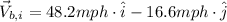
ii) Wind velocity: Vw

`\vec V_w=17mph\cdot cos(285\º)\hat i+17mph\cdot sin(285\º)\hat j`

`\vec V_w=4.4mph\cdot \hat i-16.4mph\cdot \hat j`

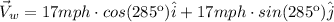
iii) Add the two velocities

Add the corresponding components:

`\vec V_b=(48.2mph+4.4mph)\cdot \hat i+(-16.6mph-16.4mph)\cdot \hat j`

`\vec V_b=52.6mph\hat i-33.0mph\hat j`